Le Peintre Fou - Trouble bipolaire

Un article de Wikipédia, l'encyclopédie libre.

Cet article est une ébauche concernant l'épistémologie et les sciences cognitives. Vous pouvez partager vos connaissances en l’améliorant. (Comment ?).

Cet article a besoin d'être illustré. Pour améliorer cet article, des médias (images, vidéos, sons) libres de droit sont bienvenues (en discuter). Vous pouvez y contribuer en en apportant (voir à ce sujet l'aide pour l'importation de fichiers).

Cet article a une forme trop académique. La forme ressemble trop à un extrait de cours et nécessite d'être réécrit afin de correspondre aux standards de l'encyclopédie. N'hésitez pas à l'améliorer.

Selon Platon la connaissance est à l'intersection de vérités et de croyances

La théorie de la connaissance est la partie de la philosophie qui étudie la nature, les origines, les contenus, les moyens et les limites de la connaissance, en particulier de la connaissance humaine. Une grande partie des travaux qui relèvent de cette discipline sont consacrés à l'analyse de la connaissance, c'est-à-dire à la détermination de ses conditions nécessaires et suffisantes. Il s'agit plus précisément d'établir quelles relations entretient la connaissance avec la croyance et la vérité, et quelles procédures de justification permettent de distinguer une simple croyance vraie (qui peut l'être par accident) d'une véritable connaissance.

Une grande partie de cet article porte sur la théorie analytique de la connaissance, discipline philosophique qui s'est pour l'essentiel développée dans le monde anglophone^[1].

Diversité des théories de la connaissance

Les théories de la connaissance sont aussi nombreuses que les philosophes qui se sont penchés sur la question. On peut commencer par les distinguer selon les différentes conceptions de l'origine de la connaissance, et de la nature de la connaissance.

Nature de la connaissance

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Origine de la connaissance

Le philosophe empiriste (cf. John Locke, David Hume) place l'expérience sensible à l'origine de l'acquisition de la connaissance. Pour sa part, le rationaliste (cf. René Descartes, Karl Popper) la fait reposer sur l'exercice de la raison.

Il faut en effet distinguer différentes théories de la connaissance :

• empiristes
• idéalistes
• rationalistes
• réalistes
• constructivistes

Théorie classique de la connaissance

Croyance vraie justifiée

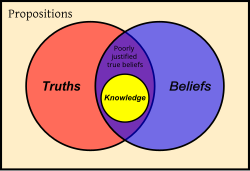
La théorie classique repose sur l'idée que la connaissance est une croyance vraie et justifiée^[2], et non seulement une croyance vraie.

Cette clause supplémentaire permet d'exclure du domaine de la connaissance les cas dans lesquels notre croyance est vraie, mais où nous ne sommes pas en mesure d'expliquer pourquoi elle est vraie. Un individu peut ainsi croire que la terre tourne autour du soleil (proposition p) par simple ouï dire, sans être capable de l'expliquer. La proposition p est vraie, mais l'individu en question ne sait pas que la terre tourne autour du soleil. Cela reste une croyance.

La justification de la croyance est donc l'élément crucial de cette analyse traditionnelle de la connaissance, et de nombreuses théories contemporaines cherchent à en déterminer précisément la nature et les modalités ; la théorie de la justification est l'une des principales branches de la théorie de la connaissance.

Le terme de « connaissance » a longtemps désigné, en philosophie, des croyances dont la vérité est justifiée de manière certaine. Toute croyance présentant un moindre degré de justification constitue à ce compte une « opinion probable » (ou connaissance par provision). Ce point de vue prévaut encore dans l'œuvre de Bertrand Russell (notamment dans les Problèmes de Philosophie, 1912). Au cours des décennies qui suivirent, l'idée selon laquelle le degré de justification des croyances doit s'évaluer en termes de certitude a perdu en influence.

Le problème de Gettier et les analyses contemporaines de la connaissance

Dans son célèbre article de 1963 intitulé « Is Justified True Belief Knowledge? », Edmund Gettier affirme qu'il existe des situations dans lesquelles une croyance peut être à la fois vraie et justifiée, et ne constitue pas pour autant une connaissance. Plus exactement, la thèse de Gettier consiste à dire que l'analyse traditionnelle énonce les conditions nécessaires de la connaissance, mais que ces conditions ne sont pas suffisantes. Pour mieux apprécier la stratégie de Gettier et les arguments que lui opposeront ses contradicteurs, il est utile de partir de l'analyse traditionnelle. D'après celle-ci :

S sait que p si et seulement si

1. p est vrai ;
2. S croit que p ; et
3. la croyance de S dans p est justifiée.

L'attaque de Gettier repose sur deux prémisses, consistantes avec l'analyse traditionnelle. Première prémisse : il est possible qu'une croyance justifiée soit fausse. (En d'autres termes, il est possible d'avoir de bonnes raisons de croire dans la vérité de p et que p soit fausse.) Seconde prémisse : si S est justifié à croire que p et que p implique q, et si S déduit q de p et accepte q comme un résultat, alors S est justifié à croire que q. À partir de ces prémisses, Gettier construit deux exemples qui manifestent l'insuffisance de la définition traditionnelle. Il suffira d'évoquer le premier.

Smith et Jones se portent candidats pour le même poste. Smith a d'excellentes raisons de croire que la candidature de Jones sera retenue, et il sait par ailleurs que Jones a dix pièces de monnaie dans sa poche. Soit p : « Jones sera embauché et il a dix pièces dans sa poche ». On voit que deux des trois conditions traditionnelles sont déjà remplies : Smith croit que p, et il est justifié à croire que p. Considérons maintenant la proposition q : « Celui qui sera embauché a dix pièces dans sa poche ». Il est clair que p implique q ; si on suppose que Smith déduit q de p, alors (par la seconde prémisse) Smith croit que q et cette croyance est justifiée.

Maintenant, il se trouve que, contrairement à la prédiction de Smith, c'est Smith, et non Jones, qui obtient le poste. Bien qu'elle soit justifiée, p est donc fausse (cas admis par la première prémisse). Mais il se trouve que Smith, à son insu, a dix pièces de monnaie dans sa poche ; q est donc vraie. Au total, Smith croit que q, il est justifié à croire que q (par inférence à partir de p), et q, à l'insu de Smith, est vraie. Nous sommes donc dans un cas de croyance vraie justifiée qui n'est pas pour autant un cas de connaissance : Smith ne sait pas que q est vraie.

Réponses à Gettier

Depuis la publication de l'article de Gettier (dans la revue Analysis, vol. 23, 1963, pp. 121-123) un très grand nombre d'auteurs ont tenté de parvenir à une analyse de la connaissance qui puisse exclure a priori de tels exemples. Les deux stratégies les plus couramment employées consistent : a) à modifier la clause de justification retenue par Gettier, jugée trop faible ; b) ou bien à conserver la clause de justification traditionnelle mais en y ajoutant une autre, censée garantir l'ensemble de l'analyse contre les exemples de type Gettier. La solution proposée par Robert Nozick relève de la première stratégie : la clause de justification traditionnelle est remplacée par deux conditionnelles fixant la relation entre la croyance de S et la vérité du contenu de sa croyance. Selon Nozick, S sait que p si et seulement si :

1. p est vraie
2. S croit que p
3. si p est fausse, S ne croira pas que p.
4. si p est vraie, S croira que p.

Simon Blackburn a critiqué cette formulation, arguant que nous ne devrions pas admettre au rang de connaissances des croyances qui, bien qu'elles « suivent la vérité à la trace » (conformément aux exigences de Nozick), ne sont pas soutenues par des raisons appropriées. En effet, il semble possible d'imaginer des scénarios dans lesquels la croyance de S est étroitement corrélée à la vérité ou à la fausseté de p, et où S est tout à fait incapable de rendre compte de sa croyance, c'est-à-dire d'avancer des éléments de justification. En d'autres termes, la croyance vraie ne sera véritablement justifiée que si S sait pourquoi elle est vraie. Nous retrouverons plus loin cette idée selon laquelle une croyance n'est justifiée que si le sujet dispose d'un accès épistémique à la base de justification : c'est la thèse fondamentale des théories internalistes de la justification. Les théories externalistes de la justification (dont Nozick nous offre ici un premier exemple) affirment au contraire que la base de justification de nos croyances ne nous est pas nécessairement accessible ; il se peut que nos croyances ne soient pas justifiées par d'autres croyances, mais par des mécanismes fiables les reliant aux modifications de notre environnement.

Dans une autre réponse, Richard Kirkham explique que l'impossibilité de parvenir à une analyse de la connaissance qui soit parfaitement à l'abri des contre-exemples de Gettier tient au fait que seule la définition de la connaissance en vigueur depuis l'Antiquité jusqu'à Russell est véritablement satisfaisante : pour être une connaissance, une croyance ne doit pas seulement être vraie et justifiée, mais sa base de justification doit encore rendre nécessaire sa vérité. Cette contrainte constitue un critère extrêmement exigeant (si nous le retenons, la plupart de nos « connaissances empiriques » n'en sont plus), mais Kirkham remarque que des standards de connaissance très hauts n'empêchent pas d'intégrer l'ensemble de nos savoirs « faibles » à la catégorie des « croyances raisonnables ».

Si on opte pour la seconde stratégie (ajouter une quatrième clause aux trois traditionnelles), une des possibilités consiste à exiger que la justification de la croyance soit « invaincue » (undefeated). Cette nouvelle théorie, due en particulier à Keith Lehrer et à Thomas D. Paxson Jr., ne vaut pas pour toute connaissance en générale, mais seulement pour celles que ces auteurs appellent « non basiques » (nonbasic). La distinction des connaissances « basiques » et « non basiques » vise le contenu de la base de justification : si S sait que p et que la base de justification de sa croyance ne comporte pas d'autres croyances, alors sa connaissance sera dite « basique ». Cette description correspond en particulier aux connaissances perceptives non inférentielles du type : « je perçois une douleur dans ma cuisse gauche ». On voit bien que cette connaissance ne repose pas sur une autre croyance, mais dérive uniquement du contenu de mon expérience. Selon Lehhrer et Paxson, la définition traditionnelle de la connaissance rend suffisamment compte des connaissances de ce type. En revanche, si S sait que p est vrai et qu'une autre proposition q entre dans la base de justification de cette croyance, alors sa connaissance sera dite « non basique » : il s'agit ici des connaissances dites « inférentielles », c'est-à-dire des connaissances qui dépendent logiquement de la vérité d'autre croyances, plus ou moins nombreuses. Dans le cas des connaissances non basiques, une quatrième clause est requise pour que l'analyse soit à l'abri des contre-exemples : la croyance vraie et justifiée doit en outre être « invaincue » (undefeated). En d'autres termes, si S sait que p et que la base de justification de p comporte q, il ne doit y avoir aucune autre proposition r qui soit vraie et qui invalide q.

Notes et références

Voir aussi

Articles connexes

Portail de la philosophie